Why round? #

Limitations of computers #

Constraints are the rule, not the exception, when running programs on computers. Processing power, memory, data transfer – these all limit what a program can achieve.

One particular limitation is data precision when a computer does math. Take the following numbers, for example:

$$\frac{1}{3} = 0.\overline{3}$$

$$\pi = 3.14159\mathellipsis$$

First of all, storing these in their fully accurate forms would take up a lot of memory. Secondly, the only way computers can even get close to storing them is through floating-point representation¹. For the examples above, floating point can never represent their values exactly.

False precision #

Another reason to round numbers is to ensure correctness. For instance, in financial applications, the accepted level of precision is to the cents value (i.e. two decimal places). However, as computations on computations happen with financial numbers, it’s important to have consistency. Not doing so can have consequences: someone might be underpaid or they might overpay for something.

In other cases, like scientific or engineering applications, the precision is only as good as the instruments used to measure the values. If one piece of equipment has only five digits of precision, then representing a measured value as 1.0291231 is misleading.

Ways to round to integers #

Let’s look at a few approaches of rounding towards integers.

Overview ² #

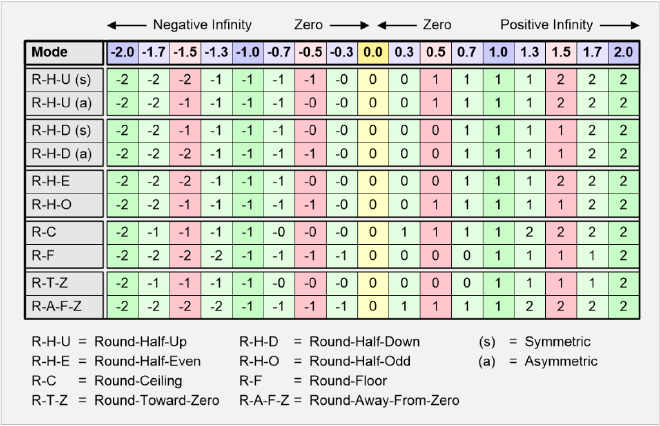
Round to the nearest integer #

This will round values towards the closest integer. This is straightforward except when the value is exactly halfway, like 2.5.

There are two ways to go, since this number is close to two integers:

• Round half up: pick the higher integer
• Round half down: pick the lower integer

Round half up seems to be the most common way to round by humans. Several programming languages use this: Java, JavaScript, and Ruby do at the very least.

Round to the higher integer (ceiling) #

This picks the integer that is immediately higher than the value.

Round to the lower integer (floor) #

This picks the integer that is immediately lower than the value. One place this comes up is with the modulo operation, where the floor is used to find the number of full divisions made before leaving a remainder.

Banker’s rounding #

This works mostly the same as the round to nearest integer methods. There’s one key distinction: the halfway values are rounded to the nearest even integer. So 2.5 rounds to 2, but 3.5 rounds to 4.

It seems quite unusual to see this method, but Python uses this for its round() function.

The main advantage is that this reduces bias. With this method, 2.5 and -2.5 would round to 2 and -2, respectively, but when using rounding half-up, 2.5 would go to 3 instead.